Ocean

Ocean modeling and turbulence

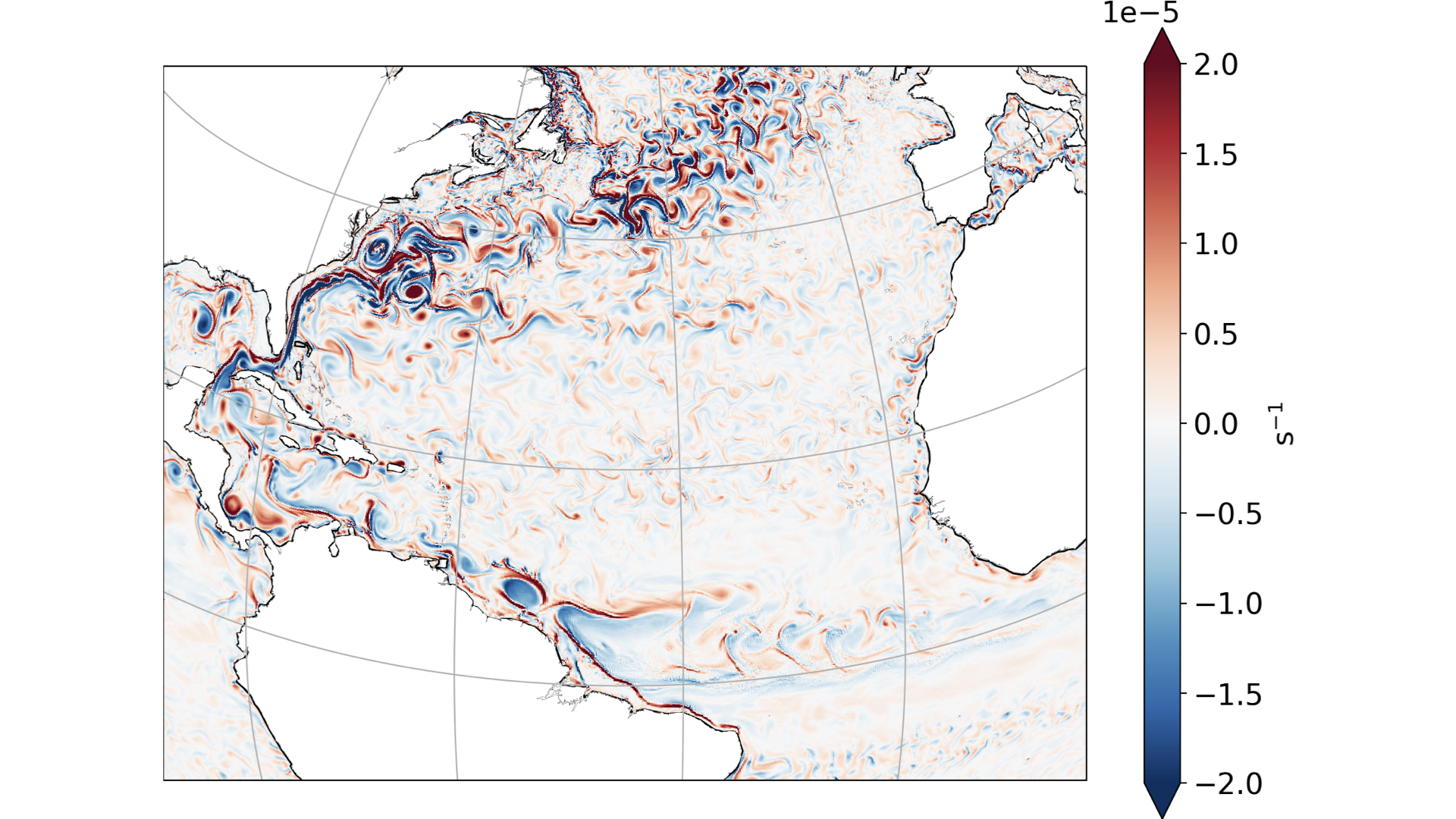
Figure: The ocean circulation is composed of many coherent features distributed over a wide range of scales. Snapshot of surface relative vorticity (swirliness) from a global 1/10 degree simulation with MOM6, showing the presence of ocean eddies, sharp boundary currents, tropical instability waves, shelf circulations, etc.

The ocean is a turbulent fluid, in which motions on a wide range of scales – from centimeters to thousands of kilometers – interact and exchange energy. Ocean turbulence plays an important role in the climate system because it can affect large-scale ocean currents as well as ocean heat uptake. Among the key features of ocean turbulence are mesoscale eddies, submesoscale eddies, and vertical mixing processes.

• Mesoscale eddies are large swirling vortices with horizontal scales typically ranging from tens to hundreds of kilometers. These eddies play an important role in the ocean energy cycle (see below) and are often associated with the meandering of ocean currents such as the Gulf Stream. Mesoscale eddies play a crucial role in transporting heat, salt, and nutrients across ocean basins.
• Submesoscale eddies have smaller horizontal scales, typically ranging from hundreds of meters to tens of kilometers, and occur in the form of fronts, filaments, and spirals. Submesoscale eddies exhibit relatively large vertical velocities, which promote the exchange of properties between the mixed layer and ocean interior and control restratification of the upper ocean boundary layer.
• Vertical mixing processes, such as turbulent diffusion and shear-induced mixing, are fundamental for redistributing heat, nutrients, and dissolved gasses throughout the water column. Mixing occurs across a range of spatial and temporal scales, from turbulent overturns driven by wind and surface waves to internal waves generated by tidal currents and density gradients.

Ocean energy cycle

The ocean energy cycle plays an important role in transporting heat, carbon, and nutrients throughout the world’s oceans, and therefore needs to be accurately represented in climate models. However, much of the ocean energy cycle is not resolved in current models because many of the important energy pathways and exchanges are driven by mesoscale eddies.

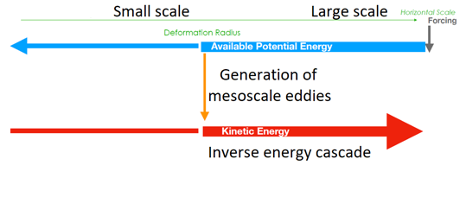
Figure: Zanna, Bachman, Jansen et al. (2020)

The schematic above shows a simplified schematic of how mesoscale eddies contribute to the the ocean energy cycle in three stages:

1. Forward Cascade of APE: Available potential energy (APE) arises from horizontal density (or buoyancy) gradients associated with variations in temperature and salinity. As mesoscale eddies form and grow, they tap into this reservoir of APE, and transfer large-scale APE to smaller scales in a forward cascade.
2. Conversion of APE to eddy KE: Near the deformation scale, where mesoscale eddies reach their maximum size and strength, a significant portion of the APE is converted into eddy kinetic energy (KE) by a process called baroclinic instability.
3. Inverse Cascade of KE: As eddies merge and interact, they transfer their kinetic energy to larger-scale structures, thus triggering a kinetic energy inverse cascade.

Parameterization in Ocean Models

Due to computational cost, the grid cells in most ocean models are not small enough to simulate ocean turbulence phenomena such as mesoscale & submesoscale eddies and vertical mixing. To still account for the effects of ocean turbulence on the resolved scales and the ocean energy cycle, one can use simplified representations of these processes: parameterizations. In M²LInES, we aim to use machine learning approaches to develop such ocean turbulence parameterizations. Specifically, we target

• Mesoscale eddy buoyancy parameterizations, which parameterize the forward cascade of APE.
• Mesoscale eddy momentum parameterizations, which parameterize the KE inverse cascade.
• Combined mesoscale eddy momentum + buoyancy parameterizations, which jointly parameterize the forward cascade of APE, the conversion of APE to eddy KE, and the KE inverse cascade.
• Submesoscale parameterizations
• Vertical mixing parameterizations