Symbolic Regression vs. Neural Networks on Multiscale L96#
To recap from the previous notebooks, Lorenz (1996) describes a “two time-scale” model in two equations which are:
This model can be visualized as follows:

Fig. 8 Visualisation of a two-scale Lorenz ‘96 system with J = 8 and K = 6. Global-scale variables (\(X_k\)) are updated based on neighbouring variables and on the local-scale variables (\(Y_{j,k}\)) associated with the corresponding global-scale variable. Local-scale variabless are updated based on neighbouring variables and the associated global-scale variable. The neighbourhood topology of both local and global-scale variables is circular. Image from Exploiting the chaotic behaviour of atmospheric models with reconfigurable architectures - Scientific Figure on ResearchGate..#
import os
import time
from IPython.display import display, SVG
import gplearn
import gplearn.genetic
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pydot
import pysindy as ps
import torch
import torch.nn.functional as F
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
from sklearn.preprocessing import PolynomialFeatures
from torch import nn, optim
from torch.utils.data import DataLoader, TensorDataset
from L96_model import L96
# Ensuring reproducibility
np.random.seed(14)
torch.manual_seed(14);
Dataset Generation#
Let’s generate some data using the same conditions as in the previous notebooks Introduction to Neural Networks and Using Neural Networks for L96 Parameterization.
Obtaining the Ground Truth#
time_steps = 20000
forcing, dt, T = 18, 0.01, 0.01 * time_steps
W = L96(8, 32, F=forcing)
X_true, _, _, subgrid_tend = W.run(dt, T, store=True, return_coupling=True)
X_true, subgrid_tend = X_true.astype(np.float32), subgrid_tend.astype(np.float32)
print(f"X_true shape: {X_true.shape}")
print(f"subgrid_tend shape: {subgrid_tend.shape}")
X_true shape: (20001, 8)
subgrid_tend shape: (20001, 8)
In this case, although we have 8 different dimensions in \(X\), each is derived in the exact same way from neighboring values of \(X\) (and local subdimensions \(Y\)). Therefore, we can actually reduce this problem from an 8-to-8D regression problem down to an 8-to-1D regression problem:
Dx = X_true.shape[1]
inputs = np.vstack([X_true[:, range(-i, Dx - i)] for i in range(Dx)])
targets = np.hstack([subgrid_tend[:, -i] for i in range(Dx)])
print(f"inputs shape: {inputs.shape}")
print(f"targets shape: {targets.shape}")
inputs shape: (160008, 8)
targets shape: (160008,)
Show code cell source
plt.figure(figsize=(16, 4), dpi=150)
plt.title("Multiscale L96 trajectory", fontsize=16)
for i in range(Dx):
plt.plot(inputs[:, i][:500], label=r"$x" + str(i) + "$")
plt.legend(ncol=2, fontsize=14)
plt.xlabel("Time", fontsize=16)
plt.ylabel("Value", fontsize=16)
plt.show()
Show code cell source
fig = plt.figure(figsize=(12, 6), dpi=150)
fig.suptitle("2D histograms of features vs. forcing", fontsize=16)
for i in range(Dx):
plt.subplot(2, 4, i + 1)
plt.hist2d(inputs[:, i], targets, bins=50)
plt.xlabel(f"$x_{i}$", fontsize=16)
plt.xticks(np.arange(-6, 13, 2))
plt.xlim(-8, 14)
if i % 4 == 0:
plt.ylabel("Forcing", fontsize=16)
plt.tight_layout()
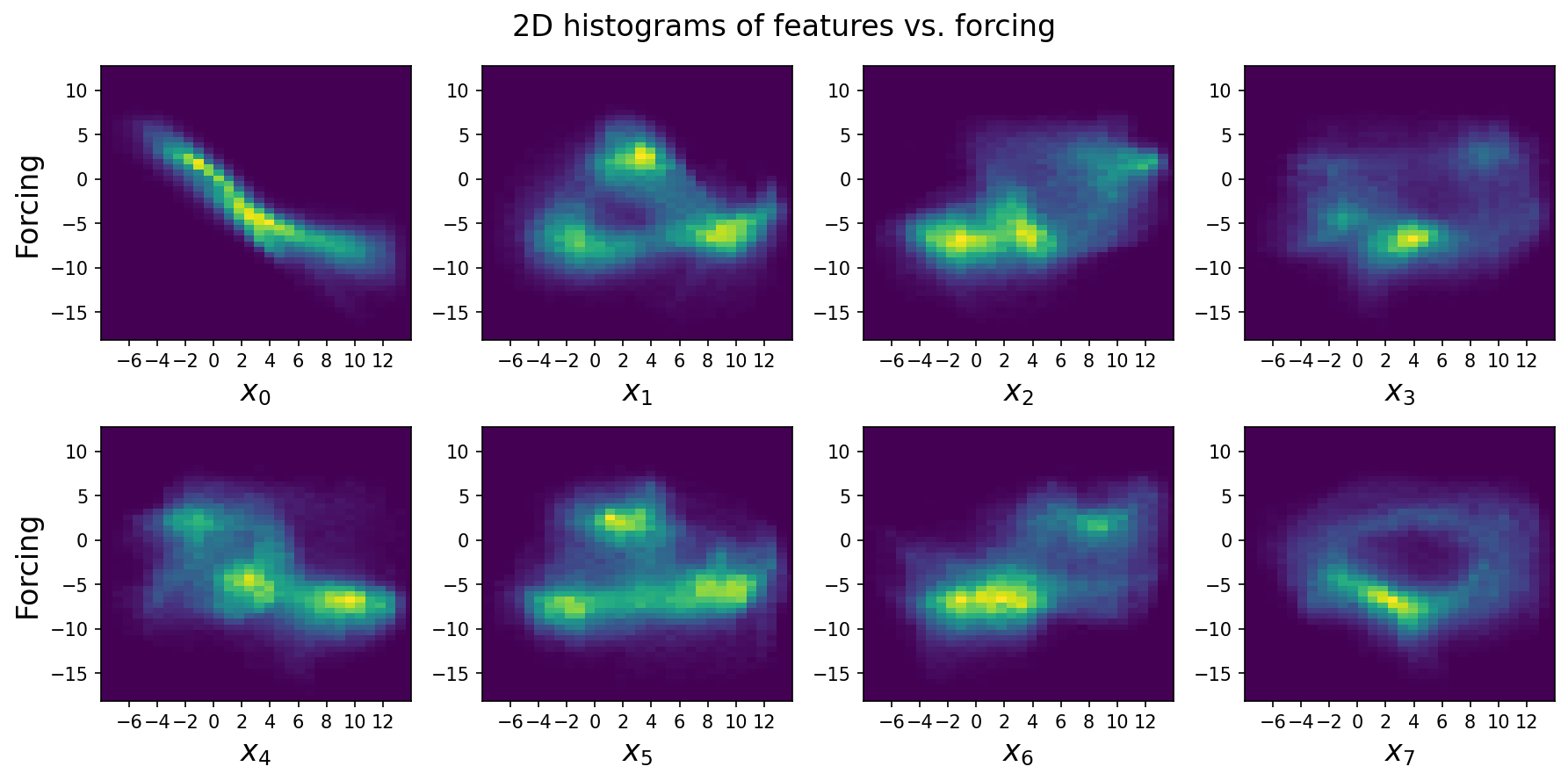
Looking at these marginal histograms of each large-scale variable vs. the subgrid forcing, we can see there’s a mostly linear relationship between \(x_0\) and its forcing, suggesting that the subgrid terms tend to force small values higher and large values lower. This suggests that an extremely simple linear model only containing \(x_0\) with negative slope will do reasonably well. However, the relationship isn’t completely linear, and also contains a bifurcation at larger \(x_0\).
For the other features, the relationships are less straightforward, but there’s clearly high mutual information.
Split the Data into Training and Test Sets#
data_idxs = np.arange(len(inputs))
np.random.shuffle(data_idxs)
num_train_samples = int(len(inputs) * 0.75)
train_idxs = data_idxs[:num_train_samples]
test_idxs = data_idxs[num_train_samples:]
Build the Dataset and the Dataloaders#
BATCH_SIZE = 1024
# Training Data
train_dataset = TensorDataset(
torch.tensor(inputs[train_idxs]), torch.tensor(targets[train_idxs])
)
loader_train = DataLoader(dataset=train_dataset, batch_size=BATCH_SIZE, shuffle=True)
# Test Data
test_dataset = TensorDataset(
torch.tensor(inputs[test_idxs]), torch.tensor(targets[test_idxs])
)
loader_test = DataLoader(dataset=test_dataset, batch_size=BATCH_SIZE, shuffle=True)
Creating and Training the Neural Network#
Now let’s create a neural network and train it on the dataset we generated above.
Define Functions to Train and Evaluate the Model#
Note
The code in this section is taken from the notebook Introduction to Neural Networks.
Show code cell content
def train_model(network, criterion, loader, optimizer):
"""Train the network for one epoch"""
network.train()
train_loss = 0
for batch_x, batch_y in loader:
# Get predictions
if len(batch_x.shape) == 1:
# This if block is needed to add a dummy dimension if our inputs are 1D
# (where each number is a different sample)
prediction = torch.squeeze(network(torch.unsqueeze(batch_x, 1)))
else:
prediction = network(batch_x)
# Compute the loss
loss = criterion(prediction, batch_y)
train_loss += loss.item()
# Clear the gradients
optimizer.zero_grad()
# Backpropagation to compute the gradients and update the weights
loss.backward()
optimizer.step()
return train_loss / len(loader)
def test_model(network, criterion, loader):
"""Test the network"""
network.eval() # Evaluation mode (important when having dropout layers)
test_loss = 0
with torch.no_grad():
for batch_x, batch_y in loader:
# Get predictions
if len(batch_x.shape) == 1:
# This if block is needed to add a dummy dimension if our inputs are 1D
# (where each number is a different sample)
prediction = torch.squeeze(network(torch.unsqueeze(batch_x, 1)))
else:
prediction = network(batch_x)
# Compute the loss
loss = criterion(prediction, batch_y)
test_loss += loss.item()
# Get an average loss for the entire dataset
test_loss /= len(loader)
return test_loss
def fit_model(network, criterion, optimizer, train_loader, val_loader, n_epochs):
"""Train and validate the network"""
train_losses, val_losses = [], []
start_time = time.time()
for epoch in range(1, n_epochs + 1):
train_loss = train_model(network, criterion, train_loader, optimizer)
val_loss = test_model(network, criterion, val_loader)
train_losses.append(train_loss)
val_losses.append(val_loss)
end_time = time.time()
print(f"Training completed in {int(end_time - start_time)} seconds.")
return train_losses, val_losses
Create the Neural Network#
class Net_ANN(nn.Module):
def __init__(self):
super(Net_ANN, self).__init__()
self.linear1 = nn.Linear(8, 16)
self.linear2 = nn.Linear(16, 16)
self.linear3 = nn.Linear(16, 1)
def forward(self, x):
x = F.relu(self.linear1(x))
x = F.relu(self.linear2(x))
x = self.linear3(x)[:, 0]
return x
Train the Network#
nn_3l = Net_ANN()
n_epochs = 20
criterion = torch.nn.MSELoss()
optimizer = optim.Adam(nn_3l.parameters(), lr=0.01)
train_loss, validation_loss = fit_model(
nn_3l, criterion, optimizer, loader_train, loader_test, n_epochs
)
Training completed in 17 seconds.
Visualize Results#
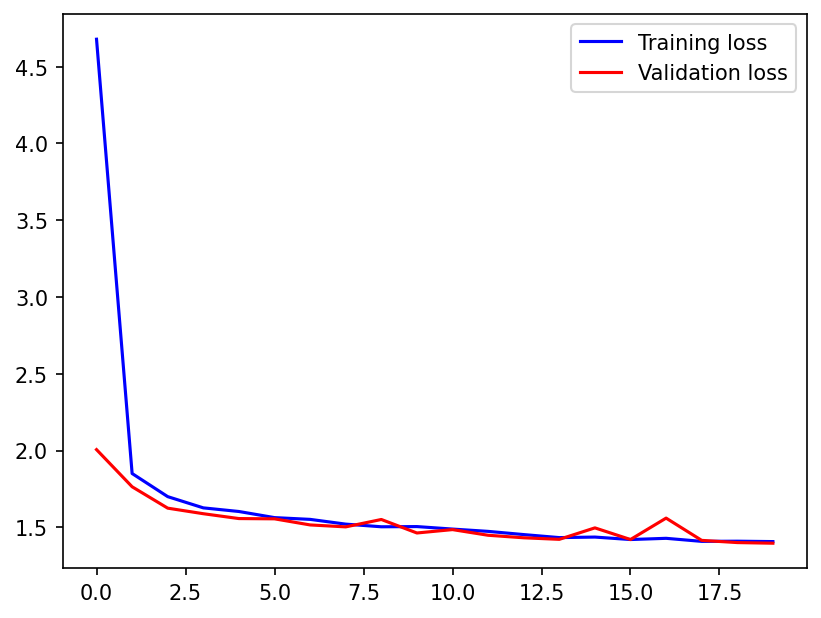
plt.figure(dpi=150)
plt.plot(train_loss, "b", label="Training loss")
plt.plot(validation_loss, "r", label="Validation loss")
plt.legend();
preds_nn = nn_3l(torch.from_numpy(inputs[test_idxs])).detach().numpy()
print("R2 Score:", r2_score(preds_nn, targets[test_idxs]))
R2 Score: 0.9223949649031744
The neural network gets an \(R^2\) of ~ 0.916, which seems pretty good given the non-determinism of the problem.
Comparing with Linear Regression#
linear_reg = LinearRegression()
linear_reg.fit(inputs[train_idxs], targets[train_idxs])
print("R2 Score:", linear_reg.score(inputs[test_idxs], targets[test_idxs]))
R2 Score: 0.8160184487760795
Linear regression also does fairly well, though about 0.1 lower in terms of \(R^2\). Lets look at its coefficients:
plt.figure(dpi=150)
plt.bar(range(8), linear_reg.coef_)
plt.xticks(range(8), [f"x{i}" for i in range(8)], fontsize=12)
plt.ylabel("Coefficient value", fontsize=12)
plt.show()
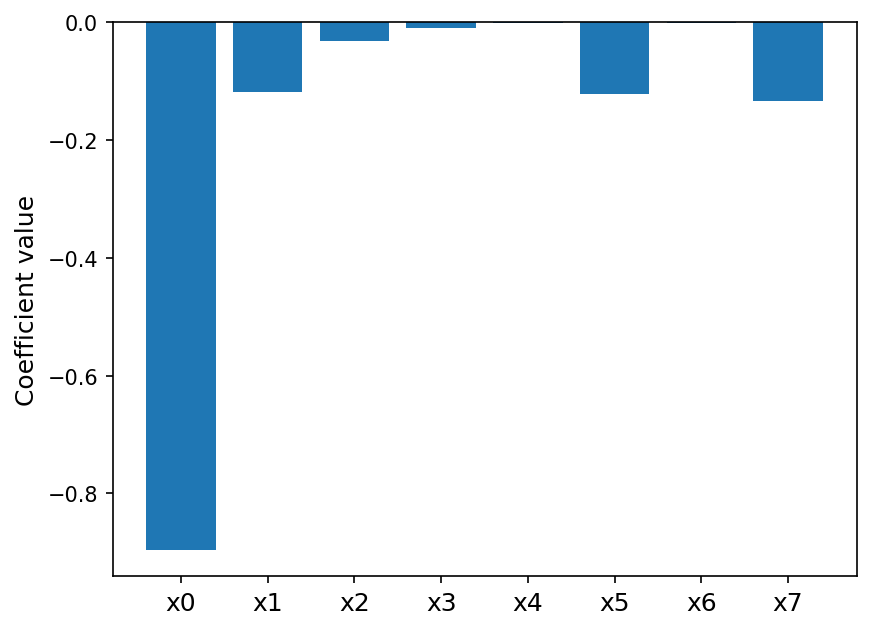
This matches the 2D histogram plots from earlier that showed a negative linear relationship between forcing and \(x_0\).
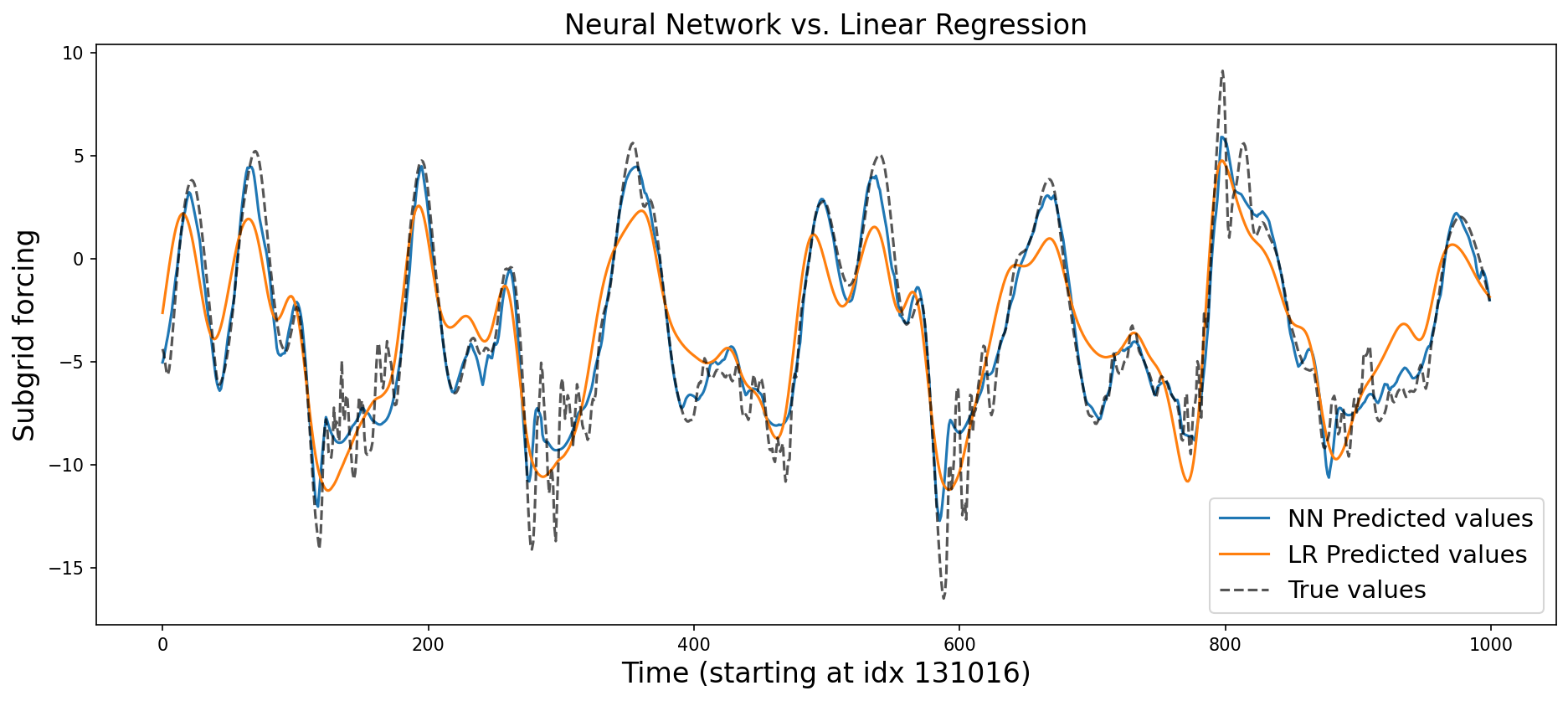
plt.figure(figsize=(15, 6), dpi=150)
plt.title("Neural Network vs. Linear Regression", fontsize=16)
preds_nn = nn_3l(torch.from_numpy(inputs)).detach().numpy()
preds_lr = linear_reg.predict(inputs)
random_idx = np.random.choice(len(targets - 1000))
random_slice = slice(random_idx, random_idx + 1000)
plt.plot(preds_nn[random_slice], label="NN Predicted values")
plt.plot(preds_lr[random_slice], label="LR Predicted values")
plt.plot(
targets[random_slice], label="True values", ls="--", color="black", alpha=0.667
)
plt.xlabel(f"Time (starting at idx {random_idx})", fontsize=16)
plt.ylabel("Subgrid forcing", fontsize=16)
plt.legend(fontsize=14)
plt.show()
Symbolic regression with genetic programming#
Let’s try using one of the genetic programming libraries to discover a parameterization:
symbolic_reg = gplearn.genetic.SymbolicRegressor(
population_size=5000,
generations=25,
p_crossover=0.7,
p_subtree_mutation=0.1,
p_hoist_mutation=0.05,
p_point_mutation=0.1,
max_samples=0.9,
verbose=1,
parsimony_coefficient=0.001,
const_range=(-2, 2),
function_set=("add", "mul", "sub", "div", "sin", "log"),
)
symbolic_reg.fit(inputs[train_idxs][:20000], targets[train_idxs][:20000])
| Population Average | Best Individual |
---- ------------------------- ------------------------------------------ ----------
Gen Length Fitness Length Fitness OOB Fitness Time Left
0 15.09 2250.77 3 1.64883 1.66775 3.21m
1 10.32 6.53204 5 1.62545 1.63651 3.13m
2 12.32 16.9512 5 1.62268 1.66148 3.04m
3 7.04 5.26195 20 1.57546 1.6044 2.26m
4 5.07 9.58891 24 1.55363 1.55098 1.84m
5 5.79 5.96614 21 1.51949 1.49863 1.97m
6 9.63 4.65507 17 1.50515 1.50598 2.64m
7 16.11 2.78142 28 1.47296 1.45776 3.67m
8 19.77 2.69051 28 1.4555 1.46709 3.93m
9 21.42 2.80303 41 1.45297 1.48639 3.84m
10 22.63 2.61995 37 1.44204 1.47566 3.98m
11 23.78 2.29202 41 1.42739 1.4853 3.87m
12 24.47 6.6118 8 1.41676 1.43687 3.60m
13 25.15 2.55741 22 1.4201 1.47976 3.29m
14 25.67 2.27797 28 1.41595 1.43681 2.97m
15 24.77 2.45272 42 1.35228 1.38372 2.61m
16 20.61 3.97112 23 1.34902 1.34875 2.02m
17 12.16 3.66793 24 1.33076 1.35901 1.30m
18 14.17 3.62681 24 1.32406 1.35392 1.30m
19 27.37 2.86559 29 1.31132 1.33767 1.82m
20 25.82 2.40423 31 1.30332 1.33496 1.41m
21 23.41 2.45246 38 1.30026 1.32775 59.04s
22 23.45 2.57487 38 1.29615 1.31448 38.19s
23 24.97 2.56582 33 1.29189 1.30837 19.99s
24 24.11 2.33584 37 1.29417 1.32678 0.00s
sub(sin(mul(-0.447, X0)), sub(X0, sin(sub(-1.107, log(add(X2, sub(sub(sub(-1.107, log(add(X2, sub(sin(sub(-1.107, log(mul(-0.447, X0)))), sub(X0, -0.220))))), X0), log(sin(mul(-0.447, X0))))))))))In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
sub(sin(mul(-0.447, X0)), sub(X0, sin(sub(-1.107, log(add(X2, sub(sub(sub(-1.107, log(add(X2, sub(sin(sub(-1.107, log(mul(-0.447, X0)))), sub(X0, -0.220))))), X0), log(sin(mul(-0.447, X0))))))))))
print(symbolic_reg._program)
sub(sin(mul(-0.447, X0)), sub(X0, sin(sub(-1.107, log(add(X2, sub(sub(sub(-1.107, log(add(X2, sub(sin(sub(-1.107, log(mul(-0.447, X0)))), sub(X0, -0.220))))), X0), log(sin(mul(-0.447, X0))))))))))
print(
"R2 Score:", r2_score(symbolic_reg.predict(inputs[test_idxs]), targets[test_idxs])
)
R2 Score: 0.8499308040527297
While the program does slightly better than linear regression, it’s extremely complicated (graph visualization below for slightly easier inspection):
# Build the graph
graph = pydot.graph_from_dot_data(symbolic_reg._program.export_graphviz())[0]
graph.write_svg("figs/symbolic_regression.svg")
# Display the graph
display(SVG("figs/symbolic_regression.svg"))
Explore the Pareto frontier#
We can explore the Pareto frontier of the final population of programs as well, to see if there’s a simpler program that still does well
df = pd.DataFrame.from_dict(
[
dict(
idx=i,
expr=str(p),
fitness=p.fitness_,
length=p.length_,
r2_score=r2_score(p.execute(inputs[test_idxs]), targets[test_idxs]),
)
for i, p in enumerate(symbolic_reg._programs[-1])
]
)
pareto_frontier = []
used_programs = set()
for l in range(1, 40):
programs = df[df.length <= l]
best = programs.r2_score.argmax()
idx = programs.idx.values[best]
r2 = programs.r2_score.values[best]
program = symbolic_reg._programs[-1][idx]
if program not in used_programs:
pareto_frontier.append(dict(length=l, r2=r2, expr=str(program)))
used_programs.add(program)
pd.set_option("max_colwidth", 200)
pareto_frontier = pd.DataFrame.from_dict(pareto_frontier)
pareto_frontier
| length | r2 | expr | |
|---|---|---|---|
| 0 | 1 | 0.000000 | -0.220 |
| 1 | 2 | 0.000000 | sin(-1.107) |
| 2 | 3 | 0.787718 | sub(-0.220, X0) |
| 3 | 8 | 0.837378 | sub(sin(mul(-0.447, X0)), sub(X0, -0.220)) |
| 4 | 11 | 0.841150 | sub(sin(mul(-0.447, X0)), sub(X0, sin(mul(-0.447, X0)))) |
| 5 | 12 | 0.842545 | sub(sin(sin(mul(-0.447, X0))), sub(X0, sin(mul(-0.447, X0)))) |
| 6 | 13 | 0.843272 | sub(sin(sin(mul(-0.447, X0))), sub(X0, sin(sin(mul(-0.447, X0))))) |
| 7 | 16 | 0.854240 | sub(sin(mul(-0.447, X0)), sub(X0, sin(sub(-1.107, log(add(X2, div(X0, -1.107))))))) |
| 8 | 17 | 0.855131 | sub(sin(sub(-1.107, log(add(X2, sub(sin(X0), X0))))), sub(X0, sin(mul(-0.447, X0)))) |
| 9 | 19 | 0.856080 | sub(sin(sub(-1.107, log(add(X2, sub(sub(sin(X0), X0), -1.107))))), sub(X0, sin(mul(-0.447, X0)))) |
| 10 | 21 | 0.856531 | sub(sin(sub(-1.107, log(add(X2, sub(sub(-0.447, X0), log(sub(X0, -0.220))))))), sub(X0, sin(mul(-0.307, X0)))) |
| 11 | 23 | 0.856728 | sub(sin(sub(-1.107, log(add(X2, sub(sub(sin(X0), X0), log(sin(mul(-0.447, X0)))))))), sub(X0, sin(mul(-0.447, X0)))) |
| 12 | 35 | 0.856754 | sub(sin(sub(-1.107, log(add(X2, sub(sin(sub(-1.107, log(add(X2, sub(sub(sin(-0.605), X0), log(sub(X0, -0.220))))))), sub(X0, sin(mul(-0.447, X0)))))))), sub(X0, sin(mul(-0.447, X0)))) |
| 13 | 39 | 0.857035 | sub(sin(mul(-0.447, X0)), sub(X0, sin(sub(-1.107, log(add(X2, sub(sub(sin(sub(-1.107, log(add(X2, sub(sub(-0.605, X0), log(sub(-0.447, X0))))))), sub(X0, sin(mul(-0.447, X0)))), log(mul(-0.447, X0... |
Unfortunately, nothing really jumps out here as both simple and performant.
Symbolic Regression with Sparse Linear Regression and Polynomial Features#
We can also apply sparse regression methods to this problem with polynomial features
def learned_expr(coef, names, cutoff=1e-3):
coef_idx = np.argwhere(np.abs(coef) > cutoff)[:, 0]
sort_order = reversed(np.argsort(np.abs(coef[coef_idx])))
return " + ".join(
[
f"{coef[coef_idx[i]]:.4f}*{names[coef_idx[i]].replace(' ','*')}"
for i in sort_order
]
)
pf = PolynomialFeatures(2)
feats = pf.fit_transform(inputs)
names = pf.get_feature_names_out([f"x_{i}" for i in range(8)])
Non-sparse linear regression#
linear_reg = LinearRegression()
linear_reg.fit(feats[train_idxs], targets[train_idxs])
learned_expr(linear_reg.coef_, names)
'-0.6913*x_0 + 0.4333*x_1 + 0.3393*x_7 + 0.2112*x_5 + 0.1420*x_6 + 0.1118*x_2 + -0.0399*x_0*x_1 + -0.0333*x_0*x_2 + -0.0323*x_6*x_7 + -0.0288*x_0*x_7 + -0.0283*x_1*x_2 + -0.0248*x_1*x_5 + -0.0242*x_3 + -0.0219*x_1*x_6 + -0.0209*x_5*x_7 + 0.0201*x_0^2 + -0.0185*x_1*x_4 + -0.0135*x_0*x_5 + 0.0124*x_0*x_3 + 0.0107*x_4 + 0.0099*x_1*x_3 + 0.0090*x_2*x_5 + -0.0088*x_4*x_7 + -0.0081*x_5^2 + -0.0076*x_2*x_3 + -0.0074*x_2*x_7 + 0.0071*x_3*x_4 + 0.0071*x_4*x_5 + -0.0069*x_3*x_5 + 0.0061*x_3*x_6 + 0.0059*x_1*x_7 + -0.0057*x_7^2 + 0.0050*x_3^2 + -0.0048*x_0*x_4 + -0.0045*x_1^2 + -0.0036*x_0*x_6 + -0.0036*x_3*x_7 + 0.0034*x_2^2 + 0.0024*x_4*x_6 + 0.0023*x_2*x_4 + 0.0015*x_2*x_6 + -0.0011*x_5*x_6'
print("R2 Score:", linear_reg.score(feats[test_idxs], targets[test_idxs]))
R2 Score: 0.8872654640415502
Adding polynomial features brings our \(R^2\) much closer to that of the neural network, but we have a ton of terms. Let’s try making the regression sparser.
Sequentially thresholded least squares#
stlsq = ps.optimizers.stlsq.STLSQ(alpha=0.001, threshold=0.01)
stlsq.fit(feats[train_idxs], targets[train_idxs])
learned_expr(stlsq.coef_[0], names)
'-3.7208*1 + -0.7842*x_0 + 0.3574*x_1 + 0.2431*x_7 + 0.1900*x_2 + 0.1778*x_5 + 0.1522*x_6 + -0.0390*x_0*x_1 + -0.0356*x_0*x_2 + -0.0335*x_6*x_7 + 0.0267*x_0^2 + -0.0265*x_1*x_5 + -0.0257*x_0*x_7 + -0.0227*x_1*x_2 + 0.0189*x_4 + -0.0164*x_1*x_6 + -0.0156*x_5*x_7 + 0.0145*x_3 + -0.0120*x_0*x_5 + 0.0110*x_0*x_3'
stlsq.score(feats[test_idxs], targets[test_idxs])
0.882294259449451
Looks like we can get a much sparser expression without sacrificing too much performance, though if we increase the threshold slightly, we will see a trade-off:
stlsq2 = ps.optimizers.stlsq.STLSQ(alpha=0.001, threshold=0.02)
stlsq2.fit(feats[train_idxs], targets[train_idxs])
learned_expr(stlsq2.coef_[0], names)
'-1.5860*1 + -0.9857*x_0 + 0.1324*x_2 + 0.0728*x_3 + -0.0725*x_7 + -0.0436*x_1 + -0.0322*x_0*x_2 + 0.0307*x_0^2'
stlsq2.score(feats[test_idxs], targets[test_idxs])
0.861645175881121
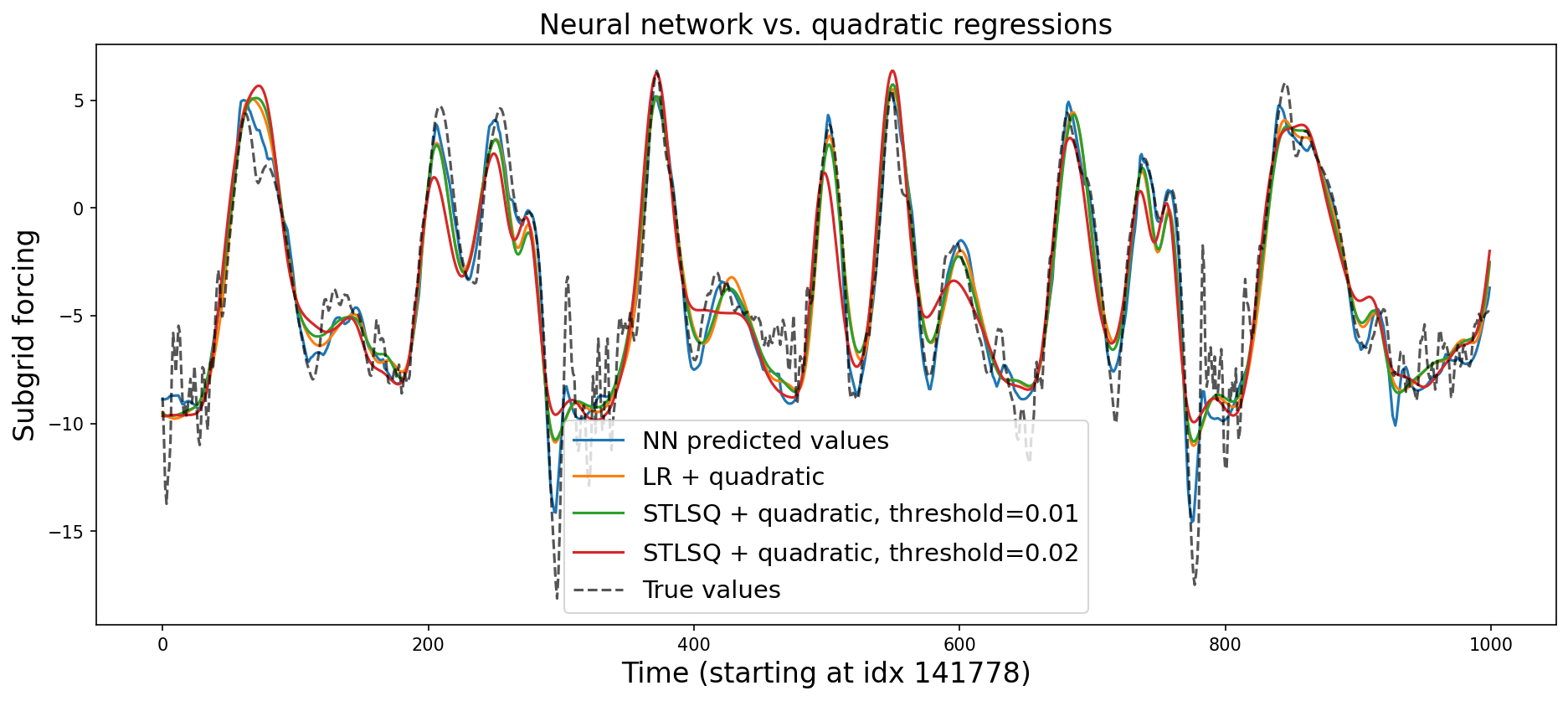
This is much simpler, but less performant. It still strongly outperformed the particluar genetic programming method we used, though. Let’s visualize some of the predictions:
plt.figure(figsize=(15, 6), dpi=150)
plt.title("Neural network vs. quadratic regressions", fontsize=16)
preds_nn = nn_3l(torch.from_numpy(inputs)).detach().numpy()
preds_lr_quad = linear_reg.predict(feats)
preds_st_quad = stlsq.predict(feats)
preds_st_quad2 = stlsq2.predict(feats)
random_idx = np.random.choice(len(targets - 1000))
random_slice = slice(random_idx, random_idx + 1000)
plt.plot(preds_nn[random_slice], label="NN predicted values")
plt.plot(preds_lr_quad[random_slice], label="LR + quadratic")
plt.plot(preds_st_quad[random_slice], label=r"STLSQ + quadratic, threshold=$0.01$")
plt.plot(preds_st_quad2[random_slice], label=r"STLSQ + quadratic, threshold=$0.02$")
plt.plot(
targets[random_slice], label="True values", ls="--", color="black", alpha=0.667
)
plt.xlabel(f"Time (starting at idx {random_idx})", fontsize=16)
plt.ylabel("Subgrid forcing", fontsize=16)
plt.legend(fontsize=14)
plt.show()
Add threshold features#
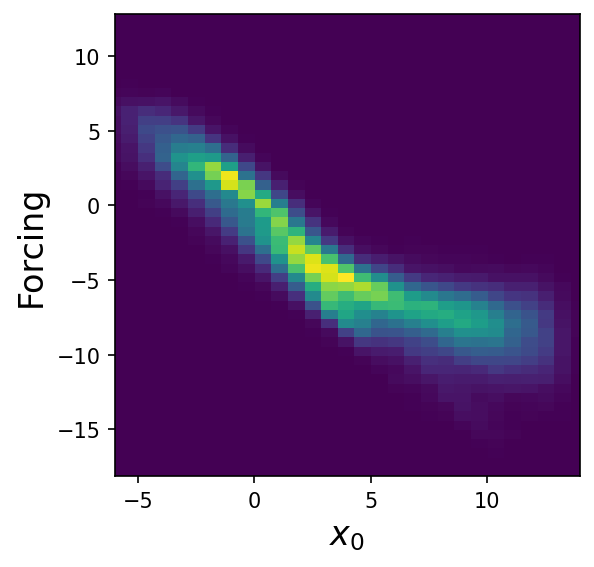
The 2D histogram of \(x_0\) looks like it might be potentially modelable by piecewise linear regression:
plt.figure(figsize=(4, 4), dpi=150)
plt.hist2d(inputs[:, 0], targets, bins=50)
plt.xlim(-6, 14)
plt.xlabel("$x_0$", fontsize=16)
plt.ylabel("Forcing", fontsize=16)
plt.show()
Sparse regression#
Let’s see if sparse regression will discover that if we provide it with thresholding features and cross-terms:
x0_thresholds = np.array(
[np.ones_like(inputs[:, 0])] + [inputs[:, 0] > i for i in range(6)]
)
x0_threshold_names = [""] + [f"*(x0>{t})" for t in range(6)]
feats2 = np.array(
[
feats[:, i] * x0_thresholds[j]
for i in range(feats.shape[1])
for j in range(len(x0_thresholds))
]
).T
names2 = [
f"{names[i]}{x0_threshold_names[j]}"
for i in range(feats.shape[1])
for j in range(len(x0_thresholds))
]
stlsq3 = ps.optimizers.stlsq.STLSQ(alpha=0.001, threshold=0.25)
stlsq3.fit(feats2[train_idxs], targets[train_idxs])
learned_expr(stlsq3.coef_[0], names2)
/usr/share/miniconda/envs/L96M2lines/lib/python3.9/site-packages/sklearn/utils/extmath.py:189: RuntimeWarning: invalid value encountered in matmul
ret = a @ b
'-2.8051*1*(x0>4) + -0.9871*x_0 + -0.6571*1*(x0>2) + 0.6440*x_0*(x0>4) + -0.5681*1*(x0>0) + -0.5286*1*(x0>1) + -0.2734*1*(x0>5)'
stlsq3.score(feats2[test_idxs], targets[test_idxs])
0.8590951075317006
plt.figure(figsize=(4, 4), dpi=150)
plt.hist2d(inputs[:, 0], targets, bins=50)
fn = (
lambda x0: -2.1200 * 1 * (x0 > 2)
+ -1.2695 * 1 * (x0 > 0)
+ -0.9488 * x0
+ -0.6694 * 1 * (x0 > 4)
+ 0.5175 * x0 * (x0 > 1)
)
xt = np.linspace(-6, 14, 100)
yt = fn(xt)
plt.plot(xt, yt, color="red")
plt.xlim(-6, 14)
plt.xlabel("$x_0$", fontsize=16)
plt.ylabel("Forcing", fontsize=16)
plt.show()
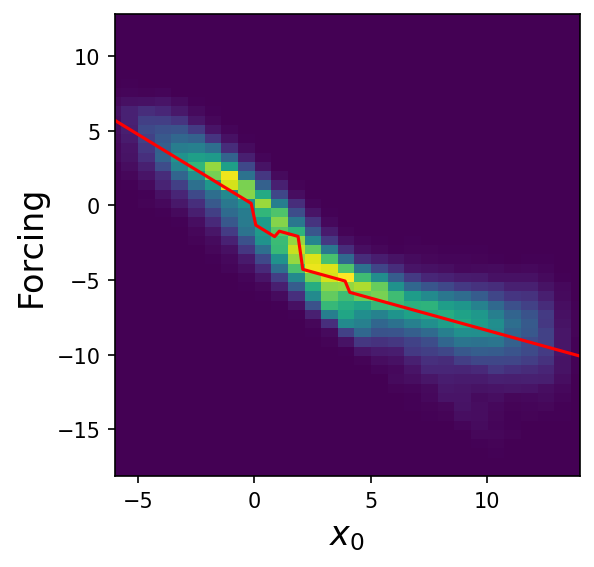
It looks like the model learns a piecewise linear function in a single variable, even though we didn’t explicitly require it!
Genetic programming#
We can also try using genetic programming here, but with a different function set that removes some of the nonlinear operators we included before and replaces them with min and max, which allow for piecewise behavior:
symbolic_reg_pw = gplearn.genetic.SymbolicRegressor(
population_size=5000,
generations=50,
p_crossover=0.7,
p_subtree_mutation=0.1,
p_hoist_mutation=0.05,
p_point_mutation=0.1,
max_samples=0.9,
verbose=1,
parsimony_coefficient=0.001,
const_range=(-2, 2),
function_set=("add", "mul", "max", "min"),
)
symbolic_reg_pw.fit(inputs[train_idxs][:20000], targets[train_idxs][:20000])
| Population Average | Best Individual |
---- ------------------------- ------------------------------------------ ----------
Gen Length Fitness Length Fitness OOB Fitness Time Left
0 27.65 3.78741e+06 7 2.45249 2.54746 5.82m
1 8.00 9.51443 5 1.85843 1.82615 4.05m
2 10.82 7.30098 3 1.6483 1.63764 4.45m
3 8.34 27.6089 3 1.64321 1.68342 4.14m
4 4.92 26.8323 15 1.50401 1.50866 3.69m
5 3.87 16.3644 15 1.44304 1.44976 3.60m
6 6.13 148.18 11 1.40594 1.42375 3.78m
7 12.76 15.4382 13 1.37424 1.38711 4.78m
8 14.48 10.2082 13 1.3658 1.36791 4.99m
9 15.67 12.0612 21 1.35567 1.37664 5.04m
10 15.53 17917.1 23 1.3514 1.40418 4.85m
11 15.51 7.61133 29 1.35019 1.38838 4.88m
12 16.27 4.11042 19 1.34782 1.38404 4.84m
13 15.22 12.9581 23 1.34734 1.38836 4.57m
14 14.50 1540.79 17 1.34519 1.40768 4.33m
15 13.97 5.27408 17 1.34517 1.40786 4.14m
16 14.09 13.3842 17 1.34172 1.43891 4.13m
17 14.21 3.51828 13 1.34363 1.37425 3.95m
18 14.46 84.8708 19 1.34315 1.43713 3.80m
19 14.50 8.1359 15 1.33915 1.37526 3.66m
20 14.49 4.71403 15 1.33942 1.41217 3.55m
21 14.12 4.65016 15 1.33662 1.39804 3.38m
22 13.77 38.3175 19 1.33467 1.42346 3.31m
23 13.67 9.76407 17 1.33539 1.41711 3.10m
24 13.87 9.07149 15 1.33255 1.43467 3.00m
25 14.14 114.952 15 1.33405 1.42116 2.88m
26 14.53 110.894 15 1.33412 1.42058 2.78m
27 14.70 3.25037 19 1.33509 1.41981 2.68m
28 14.72 10.7036 13 1.33059 1.37007 2.62m
29 14.88 3.91762 25 1.32809 1.37427 2.45m
30 14.62 6.29094 15 1.32687 1.39063 2.30m
31 14.57 3.5343 17 1.3249 1.40442 2.18m
32 14.12 3.90761 21 1.32425 1.41418 2.05m
33 13.83 5.69476 13 1.32439 1.42588 1.97m
34 13.48 8.32606 15 1.32568 1.40132 1.78m
35 13.25 79.5995 17 1.32476 1.40569 1.66m
36 13.24 4.45101 13 1.32515 1.41905 1.55m
37 13.04 7.14949 13 1.32524 1.4182 1.41m
38 13.15 5.93211 15 1.32344 1.42146 1.31m
39 13.15 9.69874 17 1.32478 1.40562 1.22m
40 13.18 5.74077 13 1.32703 1.40212 1.07m
41 12.99 9.94645 13 1.32421 1.42748 56.92s
42 12.99 4.36878 13 1.32517 1.41883 49.86s
43 13.12 12.7419 13 1.32593 1.41204 42.96s
44 13.26 3.95264 13 1.32416 1.42798 35.94s
45 13.06 13.1207 21 1.32404 1.42906 29.54s
46 13.04 6.56359 13 1.32464 1.42364 21.41s
47 13.19 6.23439 21 1.32029 1.34429 14.35s
48 13.10 27.2948 21 1.32101 1.33781 7.18s
49 13.26 5.91966 21 1.31816 1.36342 0.00s
add(max(min(mul(max(X0, -1.442), -0.938), X1), -1.937), mul(min(X0, add(max(X5, X3), max(X6, X4))), -0.720))In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
add(max(min(mul(max(X0, -1.442), -0.938), X1), -1.937), mul(min(X0, add(max(X5, X3), max(X6, X4))), -0.720))
print(symbolic_reg_pw._program)
add(max(min(mul(max(X0, -1.442), -0.938), X1), -1.937), mul(min(X0, add(max(X5, X3), max(X6, X4))), -0.720))
print(
"R2 Score:",
r2_score(symbolic_reg_pw.predict(inputs[test_idxs]), targets[test_idxs]),
)
R2 Score: 0.8354791875984894
While this leads to slightly higher \(R^2\) than before, the model is still pretty complex:
# Build the graph
graph = pydot.graph_from_dot_data(symbolic_reg_pw._program.export_graphviz())[0]
graph.write_svg("figs/symbolic_regression_pw.svg")
# Display the graph
from IPython.display import Image, display
display(SVG("figs/symbolic_regression_pw.svg"))
Tuning the hyperparameters could help, but requires more compute.